题目描述

给定一个数组，找出其中最小的 K 个数。例如数组元素是 4,5,1,6,2,7,3,8 这 8 个数字，则最小的 4 个数字是 1,2,3,4。如果 K > 数组的长度，那么返回一个空的数组

复习 - 堆

详细图解参考 b 站视频

什么是堆

1. 是完全二叉树

   完全二叉树：从上到下，从左到右添加节点

2. 每一颗子树的父节点大于子节点

堆的表示

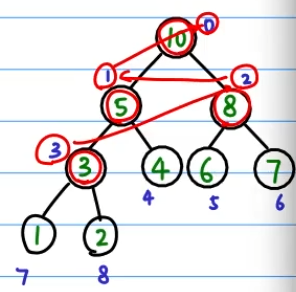
使用一维数组即可。数组元素顺序就是层次遍历堆的结果。
由于是完全二叉树，所以可以由一个节点的数组索引，准确定位其直接父节点和直接子节点。

假设从 0 开始
索引为 i 的元素在堆中对应的直接父节点为：
Math.floor((i - 1) / 2)
左孩子为：
2 * i + 1
右孩子为：
2 * i + 2

heapify

操作过程：从一个节点开始，将这个节点及其所有子节点构成的完全二叉树变为堆的过程。

这个操作不用于整个完全二叉树完全打乱的状态。

heapify 的实现：

function heapify(arr, n, i) {
    // n: 使用的 arr 长度, 从 0 开始
    // i: 当前节点的索引位置
    // arr: 一维数组表示的堆

    // 递归的结束条件
    if (i >= n) {
        return;
    }
    let max = i;
    const left = 2 * i + 1;
    const right = 2 * i + 2;
    // 比较其左右节点与自身的三个值, 得到最大值
    if (left <= n && arr[left] > arr[max]) {
        max = left;
    }
    if (right <= n && arr[right] > arr[max]) {
        max = right;
    }
    if (max !== i) {
        swap(arr, i, max);
        heapify(arr, n, max);
    } else {
        return  // max 就是 i 时不用解了, 退出
    }
}

构建堆

用于将一整个完全打乱状态的完全二叉树变为堆。

从所有叶子节点的直接父节点开始，自底向上进行 heapify 操作。

整个完全二叉树的最后一个 / 两个叶子节点的父节点可以由上面的方法得到：

Math.floor((n - 1) / 2)  // n 是数组最后元素下标。

构建堆时，所有叶子节点的直接父节点就是依次减去 1. 直到为 0

function buildHeap(arr) {
    // 需要借助 heapify 方法
    let last = arr.length - 1;
    last = Math.floor((last - 1) / 2);
    while (last >= 0) {
        heapify(arr, arr.length - 1, last);
        last -= 1;
    }
}

堆排序

构建一个升序数组：
先构建堆，此时完全二叉树的根节点是整个数组的最大值，然后每次交换完全二叉树的根节点和完全二叉树的最后一个节点，然后忽略最后一个节点进行 heapify 操作，heapify 操作后完全二叉树的根节点成为了第二大值，依次类推，当只有一个数时，就是最小值了。。。

function sortByHeap(arr) {
    buildHeap(arr);
    let n = arr.length - 1;
    const sortedArr = [];
    while (n >= 0) {
        sortedArr.push(arr[0]);
        swap(arr, 0, n);
        // 不用截断数组, 直接把 arr 长度 "改掉"
        heapify(arr, n - 1, 0);
        n -= 1;
    }
    return sortedArr;
}

解法 1：直接排序

好家伙，直接排序 + 截取数组！

function GetLeastNumbers_Solution(input, k)
{
    // write code here
    if (k > input.length) {
        return [];
    }
    let sortedArr = input.sort((a,b) => a-b);
    return sortedArr.slice(0,k);
}

• 时间复杂度：取决于 JavaScript 实现 sort 函数的方式，就算做 O(NlogN) 吧
• 空间复杂度：借助了辅助数组存储排序后的数组，明显是 O(N)

估计面试这么写会让面试官感觉比较拉🤡

解法 2：堆排序

注意题目是构建小根堆。

function GetLeastNumbers_Solution(input, k) {
    // write code here
    if (k > input.length) {
        return [];
    }
    function swap(arr, i, j) {
        const temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }

    // 从一个节点, 开始自上至下
    function heapify(arr, n, i) {
        // n: 使用的 arr 长度, 从 0 开始
        // i: 当前节点的索引位置
        // arr: 一维数组表示的堆

        // 递归的结束条件
        if (i >= n) {
            return;
        }

        let min = i;
        const left = 2 * i + 1;
        const right = 2 * i + 2;
        // 比较其左右节点与自身的三个值, 得到最大值
        if (left <= n && arr[left] < arr[min]) {
            min = left;
        }
        if (right <= n && arr[right] < arr[min]) {
            min = right;
        }
        if (min !== i) {
            swap(arr, i, min);
            heapify(arr, n, min);
        } else {
            return  // min 就是 i 时不用解了, 退出
        }
    }

    function buildHeap(arr) {
        // 需要借助 heapify 方法
        let last = arr.length - 1;
        last = Math.floor((last - 1) / 2);
        while (last >= 0) {
            heapify(arr, arr.length - 1, last);
            last -= 1;
        }
    }

    // 前 k 个
    function sortByHeap(arr, k) {
        buildHeap(arr);
        let n = arr.length - 1;
        const sortedArr = [];
        const stop = n - k;
        while (n > stop) {
            sortedArr.push(arr[0]);
            swap(arr, 0, n);
            // 不用截断数组, 直接把 arr 长度 "改掉"
            heapify(arr, n - 1, 0);
            n -= 1;
        }
        return sortedArr;
    }
    // console.log(sortByHeap(input, k));
    return sortByHeap(input, k);
}

// const arr = [7, 9, 11, 15, 17, 6, 13];
// GetLeastNumbers_Solution(arr, 3)