找出一个数,这个数需要去按照某种规则查找。
二分查找
尤其常用来在递增或递减区间中搜索目标值。
2021-7-13 补充 - 开始:
讲解视频:五点七边
新的角度:
视频中,二分查找的目的就是,找出蓝红边界出来: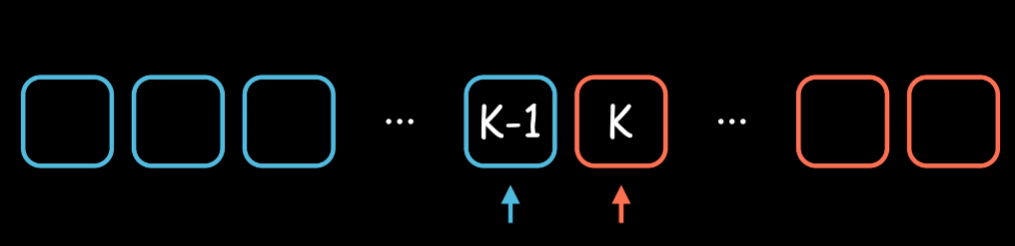
求出的未知数 k or k-1 就是解。
需要注意,视频的算法与晚上流传的代码不同:
- 两侧的指针是从
数组之外的地方作为初始值,向内移动的。
- 修改 left 与 right 时,都是直接赋值为 m。
- 返回值根据实际情况设置为 left 或者 right。
伪代码: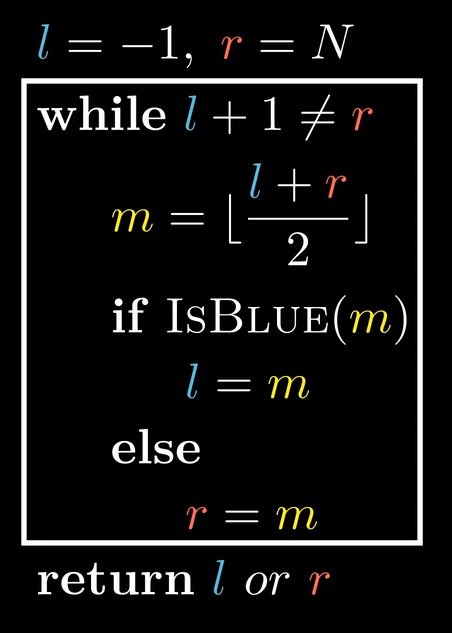
查找流程动图(动图有点大):
问 1:
为什么不初始化 left 为数组第一个值 0 或者 right 初始化为 N-1 呢?
答:考虑数组全是红色的情况,如果全为红色,left 指向的是蓝色元素,这就矛盾了。right 同理。
问 2:
中间的 mid 值是否始终在 [0,N) 内取值?
答:YES。看图
问 3:
更新 left 或者 right 时,能不能写成 mid=left+1ormid=right-1?
答:可以但没必要。不容易理解并且容易犯错。当 mid 正好在边界时,不好理解怎么 left 或者 righ 更新。
问 4:
程序会死循环吗?
答:不会。首先,left + 1 === right 时,退出循环。
left + 2 === right 时,left 或者 right 更新后变为 left + 1 === right。
left+3 === right 时,left 或者 right 更新后变为 left + 2 === right。
以此类推
总结:二分的一般流程。
2021-7-13 补充 - 结束
在最简单的形式中,二分查找对具有指定左索引和右索引的连续序列进行操作。我们也称之为查找空间。二分查找维护查找空间的左、右和中间指示符,并比较查找目标;如果条件不满足或值不相等,则清除目标不可能存在的那一半,并在剩下的一半上继续查找,直到成功为止。
当然,一般题目不太可能给你一个如此现成的题型,让你上手就可以使用二分,所以我们需要思考如何构造一个成功的二分查找:
- 预处理过程(大部分场景就是对未排序的集合进行排序)
- 二分查找过程(找到合适的循环条件,每一次将查找空间一分为二)
- 后处理过程(在剩余的空间中,找到合适的目标值)
实现二分查找解决题目时注意:
- 初始条件
- 终止
- 向左查找
- 向右查找
二分查找的题目,基本逃不出三种:找特定值,找大于特定值的元素(上界),找小于特定值的元素(下
界)。而根据这三种,代码又最终会转化为以下这些问题:
- low,high 要初始化为 0、n-1 还是 0、n 又或者是 1,n?
- 循环的判定条件是
low<high还是low <= high? - if 的判定条件应该怎么写?
- if 条件正确时,应该移动哪边的边界?
- 更新 low 和 high 时,mid 如何处理?
题目一
这里总共有 N 堆香蕉,第 i 堆中有 piles[i] 根香蕉。警卫已经离开了,将在 H 小时后回来。 阿珂可以决定她吃香蕉的速度 K (单位:根 / 小时),每个小时,她将会选择一堆香蕉,从中吃掉 K 根。如果这堆香蕉少于 K 根,她将吃掉这堆的所有香蕉,然后这一小时内不会再吃更多的香蕉。珂珂喜欢慢慢吃,但仍然想在警卫回来前吃掉所有的香蕉。返回她可以在 H 小时内吃掉所有香蕉的最小
速度 K(K 为整数)。
示例:
输入: piles = [3,6,7,11], H = 8
输出: 4
输入: piles = [30,11,23,4,20], H = 5
输出: 30
输入: piles = [30,11,23,4,20], H = 6
输出: 23
解答:化为二分查找问题。初始时,下边界就是每次吃一个,上边界就是每次吃数组最大值。要求的 k 就是每次吃 k 个,每次吃 k 个需要的小时数大于等于 h(因为 k 可能不是整数,但是题目显然要求整数,所以说解是大于等于 h 的)。

Javascript 代码为:
function eatBan(arr, h) {
function canEat(k) {
let sumH = 0;
for (let i = 0; i < arr.length; i++) {
if (arr[i] % k === 0) {
sumH += arr[i] / k;
} else {
sumH += Math.ceil(arr[i] / k);
}
}
return sumH > h;
}
let left = 1; // 存在一种可能, 立马吃完: arr=[5], h=4
let right = Math.max(...arr);
// 版本一 while
while (left < right) {
mid = Math.floor(left + (right - left) / 2);
if (canEat(mid)) { // 全吃了需要的时间 sumH 大于警卫休息时间 h, 即吃不完, 所以每次要多吃点, 增加最小值
left = mid + 1; // left 时可以取到与 right 相等的值的
} else { // 需要的时间小于警卫休息时间, 慢慢吃, 缩减最大值
right = mid; // 因为最后解出的 sumH 会大于等于 h, 所以这里不要 mid-1 !!!
}
}
// 版本二 while
while (left <= right) {
mid = Math.floor(left + (right - left) / 2);
if (canEat(mid)) {
left = mid + 1;
} else {
right = mid - 1;
}
}
// 两个版本都是返回 left
return left;
}代码解释就看注释。
假如我们的阿珂就是笨笨的,将 low 初始化成了 0,high 变为 max(...arr) + 1,此时的循环条件应该如何写?
参考 b 站那个五点七边 up 的视频
题目二
给定一个非负整数 x,计算并返回 x 的平方根。
由于返回类型是整数,所以小数位被截断,只返回结果的整数部分。
注意:不允许使用任何内置指数函数或运算符。
解答:很明显可以直接使用二分。不能用内置指数函数,乘法是可以用的。
不过要注意,由于是正整数,所以当 x 大于 1 时,sqrt(x) 取整后必定小于等于 x/2。故,若将上边界设为 x/2,对 1 和 0 进行特判即可。
JS 代码如下:
// 把 mid*mid === x 与 mid*mid < x 融合
function mySqrt2(x) {
if (x === 1) {
return x;
}
let left = 2;
let right = Math.floor(x / 2);
// 版本一的 while,上取整
while (left < right) {
let mid = Math.ceil(left + (right - left) / 2);
if (mid * mid > x) {
right = mid - 1;
} else {
left = mid;
}
}
// 版本二的 while,下取整
while (left <= right) {
let mid = Math.floor(left + (right - left) / 2);
if (mid * mid > x) {
right = mid - 1;
} else {
left = mid + 1;
}
}
// 两种版本都是返回 while
return right; // 为什么是 right?
}代码需要注意的地方:
代码二的 left 是需要搭配
left<=right,这也导致也进一步扩大了搜索空间。有些数,代码二要比代码一多计算一次。出循环时,代码二的 right 永远是比 left 小 1 的。代码一则情况不一。
为什么返回值是 right? 就版本一来说:因为
mid+1和mid-1中,若有满足条件的值,则只有可能是 mid-1.
答:mid * mid < x,假设 x 是 10,mid 是 3,解是 3,但是mid * mid < x,所以left = mid + 1后,left 就不是解了。mid * mid > x,假设 x 是 10,mid 是 4,解是 3,但是mid * mid > x,所以 mid 变为 3,就是解。我们通过不停的缩小搜索空间,最终 left 就变成我们要找的 mid 值,所以直接返回 left 就可以了。
题目三
第一个错误的版本
假设你有 n 个版本[1, 2, ..., n],你想找出导致之后所有版本出错的第一个错误的版本。
题目给定isBadVersion(version)接口来判断版本号 version 是否在单元测试中出错。实现一个函数来查找第一个错误的版本。尽量减少对调用 API 的次数。
解答:没啥好解释的。就是把比较大小直接变为了比较布尔值。。。
var solution = function(isBadVersion) {
/**
* @param {integer} n Total versions
* @return {integer} The first bad version
*/
return function(n) {
let left = 1;
let right = n;
while (left < right) {
let mid = left + Math.floor((right - left) / 2);
if (isBadVersion(mid)) {
right = mid;
} else {
left = mid+1;
}
}
console.log(left, right)
return left;
};
};题目四
剑指 Offer 的面试题三的题目二:
题目描述:
- 在长度为 1+n 的数组里,所有数字元素大小为 [1,n],显然包含至少一个重复的数字。找出其中任一重复的数字。注意,不能修改输入的数组
使用额外数组的解法就不说了,因为不是二分思想。
二分思想的解法:
看看这个 1-n 这 n 个数字,对着 n 个有序数字进行二分,每次都对一个区间内的数字到输入数组中计数。例如,若 1-k 这连续的 k 个数字在输入数组中出现的次数大于 k 次,说明,1-k 内又重复数字,可以缩小范围继续搜索。
function findDuplicate(arr) {
function counts(left, right) {
let count = 0;
for (let e of arr) {
if (e >= left && e <= right) {
count += 1;
}
}
return count;
}
let left = 1
let right = arr.length - 1;
// 从 left 到 right 是有序的
while (left <= right) {
let mid = left + Math.floor((right - left) / 2)
let count = counts(left, mid)
if (left === right) {
if (count > 1) {
return left;
} else {
return -1
}
}
if (count > (mid + 1 - left)) {
right = mid;
} else {
left = mid + 1;
}
}
}按照 B 站视频的解法模板,代码显得又比较复杂了:
function findDuplicate(arr) {
function counts(left, right) {
let count = 0;
for (let e of arr) {
if (e >= left && e <= right) {
count += 1;
}
}
return count;
}
let left = 1;
let right = arr.length - 1;
// 从 left 到 right 是有序的
while (left + 1 !== right) {
let mid = left + Math.floor((right - left) / 2)
let count = counts(left, mid)
if (count > (mid - left) + 1) {
right = mid;
} else {
left = mid;
}
}
// 确定返回 left 还是 right
if (counts(left, left) > 1) {
return left
} else if (counts(right, right) > 1) {
return right;
} else {
return -1;
}
}- 建模,红色区域和蓝色区域的意义:蓝色指针及其左边区域无重复数字;红色指针及其右边区域无重复数字。并确定用来判断的函数
counts
- 套用模板
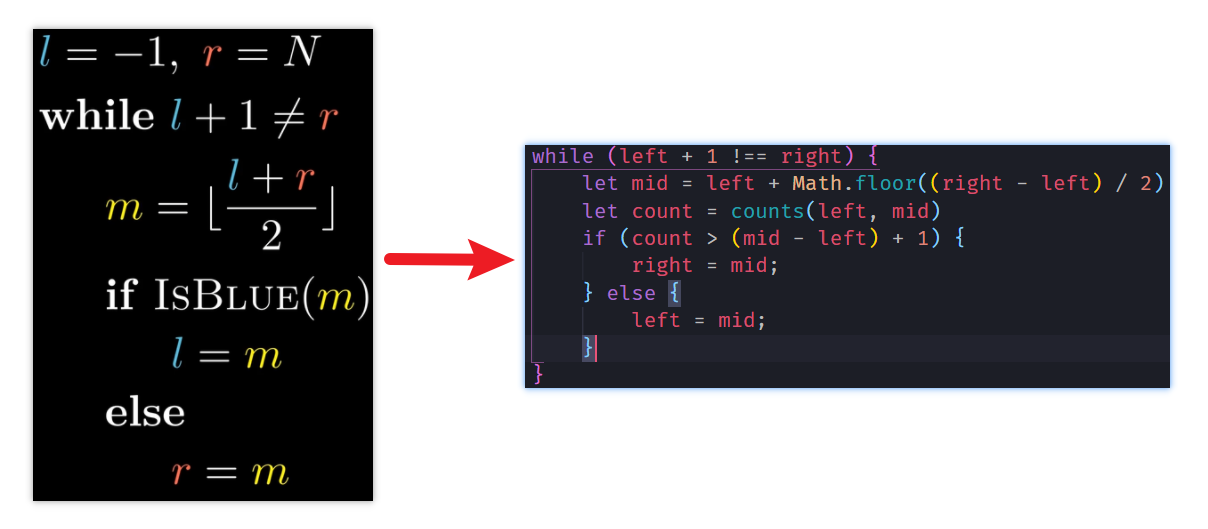
- 确定返回 left 还是 right
总结二分查找
大家一定要明确 mid 的真正含义有两层
- 我们通过 mid 值来收敛搜索空间。如题一
- 题目最后的 mid 值(或者说 left,right)就是我们要找的目标值。如题二
参考
- 和小浩学算法. pdf
转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论。